Our premise is that competitions with adversary may induce interesting and effective team strategies, as we see in many different sports as well as nature, for example, a flock of starling trying to evade from their predator.
Adversary could mean various things including cyber-physical attacks, or more generally, uncertainties or internal failures of the system. In our research, we have considered the problem of security against adversarial autonomous swarms
Security against adversarial autonomous swarms
As the large-scale deployment of multiple autonomous agents becomes more practical, maintaining security against adversarial autonomous swarms becomes important in both civilian and military defense applications. Driven by this motivation, we consider various scenarios related to perimeter defense.
Perimeter Defense Game
Scenarios with evasive targets who need to be detected, intercepted, or surrounded by other robots are often formulated as pursuit-evasion games (PEGs). The problem is to find the optimal control laws for the agents, and to identify whether capture is possible or not from a given initial condition. The problem becomes very challenging when there are multiple evaders and multiple pursuers. We formulated a variant of PEGs in which the intruder team tries to score by sending as many intruders as possible to the target area, while the defender team tries to minimize this score by intercepting them.
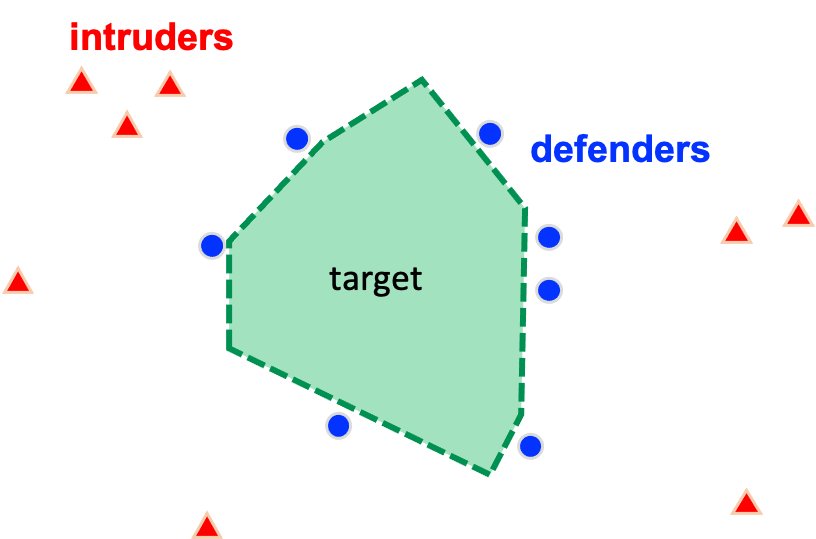
For games played between one intruder and one defender, we solved the problem for perimeters having circular shape as well as any arbitrary convex shapes.
- One vs. one problem on circular and polygonal perimeter: C-5 [CDC18]
- One vs. one problem on arbitrary convex shapes: J-5 [arXiv]
For team vs. team scenarios, we have developed a decomposition method that reduces a complex problem into smaller tractable pieces.
- Introduction of “Local Game Regions (LGR)” C-5 [CDC18]
- Using LGRs to construct team strategies; Showing Nash equilibrium in team vs. team setting: J-4 [RAL20]
We have also studied the problem of team formation when the task is to be completed by a team of patrollers and a team of defenders, potentially having heterogeneous capabilities.
- Team composition among heterogeneous agents; Patrolling strategy with guaranteed detection: C-7 [CDC2019]
Video: Patrollers (yellow) guarantee detection of intruders, and defenders maximize the number of capture.
Probabilistic Barrier Coverage
Another formulation of perimeter defense considers the placement of sensors/defenders to detect intruders. More specifically, the scenario is formulated as a barrier coverage, which aims to minimize the number of unseen paths.
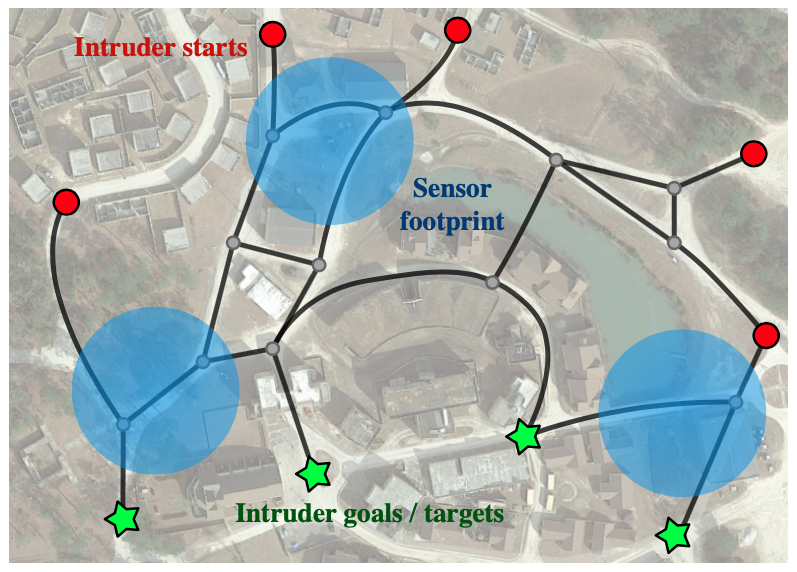
This example above shows a scenario in which intruders can select arbitrary paths from any of the start locations (red circles) to any of the goal locations (green stars). Three defenders (blue circles) are deployed to detect the intruders.
The problem becomes challenging when the number of defenders is insufficient for a full coverage, requiring us to find the most effective location to deploy them. To this end, we use ideas from game theory to account for various paths that the intruders may take. Specifically, we propose an iterative algorithm to refine the set of candidate defender formations, which uses the payoff matrix to directly evaluate the utility of different formations.
- Game theoretic formation design for probabilistic barrier coverage: C-10 [IROS20]